Linear Regression
Linear Regression is an ML algorithm based on supervised learning. It performs a regression process based on independent variables Regression models a target prediction value. It’s normally used for finding out the connection between forecasting and variables. Different regression models differ based on – the relationship type between independent and dependent variables, they’re considering and the number of independent variables being used.
Standard form of Linear equation Ax + By = C, this equation must be converted into slope-intercept form i.e. y = mx + c for easy graph implementation. Another form of equation for a line Point-slope form (y-y1) = m(x-x1), the slope m is defined above, x & y are the variables (x1 , y1) are the points on the line.
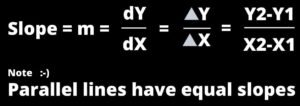
In summary,
Y = mx + c
Where c is the y-intercept (the value of y when x=0), m is the slope.
Important points to remember 🙂
- There must be a linear relationship between dependent and independent variables.
- Multi regression suffers from autocorrelation, heteroskedasticity, multicollinearity.
- It is very sensitive to Outliers. Outliers can terribly affect the regression line and also forecasted values.
- The difference between simple and multilinear regression is that multilinear regression has >1 independent variable, whereas in single linear regression there is only 1 independent variable.
- In the case of multiple independent variables, we can go with a stepwise approach, forward selection, backward elimination.
Logistics Regression
After Linear Regression, the most famous machine learning algorithm is Logistic Regression. In many ways, logistic regression and linear regression are similar. However, the difference lies in what they’re used for. Linear regression algorithms are used for predicting or forecasting values but logistic regression is used in classification tasks.
There are lots of classification tasks done regularly by people. For instance, classifying whether an email is spam or perhaps not, classifying if a tumor is benign or malignant, classifying whether a website is fraudulent or not, etc. These’re common situations where machine learning algorithms are able to make our lives a lot easier. A very simple, useful and rudimental algorithm for classification stands out as the logistic regression algorithm.
It is a supervised learning classification algorithm used for predicting the probability of a target variable. The dependent variable is binary in nature having data coded as either 0(False\No) or 1(True\Yes).
Types of Logistic Regression
- Binary or Binomial
- Multinomial
- Binary or Binomial logistic regression
In Binary or Binomial logistic regression, a dependent variable can have only two possible results i.e. either 1 or 0. There should be no outliners in the data. There should be no chance for high correlations among the predictors. These variables are used to represent win or loss, yes or no, success or failure.
- Multinomial logistic regression
In Multinomial logistic regression, a dependent variable can have more than two possible outcomes or the types representing quantitative significance. The variables can represent ‘Type A’, ‘Type B’, ‘Type C’.
Important points to remember 🙂
- It is widely used in classification problems.
- It doesn’t require a linear relationship between independent and dependent variables. It can also handle various relationships because it uses a non-linear log transformation to predict odd ratios
- All significant variables must be included to avoid fitting and under-fitting.
- It requires less input data.
- The independent variables shouldn’t be correlated with one another i.e. simply no multi-collinearity. However, we have the option to include the interaction effects of categorical variables in the analysis and in the model.
- If the dependent variable is ordinal, then it is known as Ordinal Logistic Regression
- If the value of the dependent variable is multi-class, then it is known as Multinomial Logistic regression.



